What Is A One To One Function

Understanding One to One Functions

One to one function, also known as an injective function, is a special type of function where each element in the range is mapped to exactly one element in the domain. This means that the outputs of a one to one function never repeat. For instance, if we consider the function g(x) = x – 4, it is a one to one function because each input produces a unique output. On the other hand, the function g(x) = x² is not a one to one function as it gives the same output for 2 and -2.

Defining One to One Functions

A function g: D -> F is termed one to one if g(x₁) = g(x₂) implies x₁ = x₂ for all x₁ and x₂ in D. In simpler terms, a one to one function ensures that each input has a unique output, making it an injection. This property distinguishes it from many to one functions where multiple inputs can lead to the same output.

Horizontal Line Test for One to One Functions

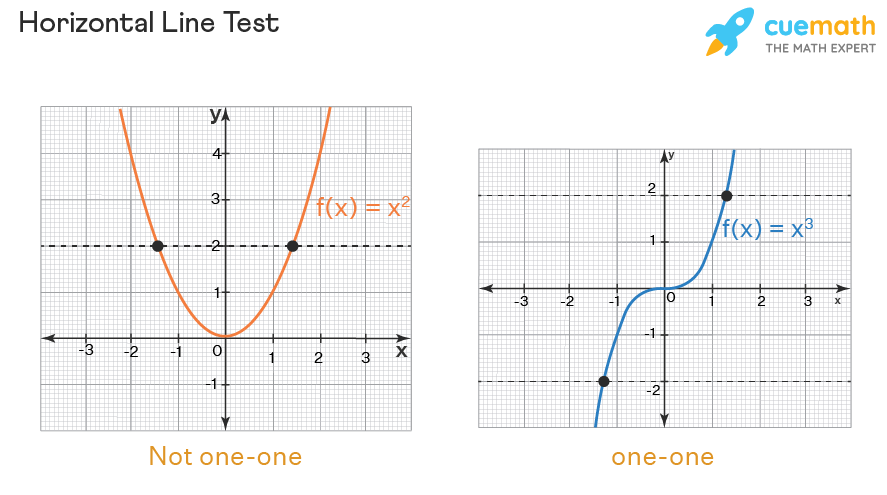
The horizontal line test is a graphical method used to determine if a function is one to one. By passing a horizontal line through the graph of a function, if the line intersects the graph at more than one point, the function is not one to one. Conversely, if the horizontal line intersects the graph at only one point at any instance, the function is classified as one to one.

Properties of One to One Functions

One to one functions exhibit several key properties:

• If two functions f(x) and k(x) are one to one, their composite function f ◦ k is also one to one.
• The domain of a one to one function g equals the range of its inverse function g^-1, and vice versa.
• A one to one function’s graph is either always increasing or always decreasing.
• The composition of a one to one function and its inverse results in the identity function.

Determining if a Function is One to One

There are various methods to ascertain if a function is one to one:

• Graphical approach: Use the horizontal line test to check if the function’s graph passes through a unique y-value each time.
• Algebraic method: Verify if a = b for every g(a) = g(b) to confirm one to one property.
• Derivative analysis: A function is one to one if its derivative is always positive or always negative throughout its domain, indicating a strictly increasing or decreasing function.

Graphical Representation of One to One Functions

When representing a one to one function graphically, each point on the graph uniquely corresponds to an x-value without repetition. This characteristic ensures that no horizontal line intersects the graph more than once, validating its one to one nature.

Inverse of One to One Functions

The concept of the inverse function is closely tied to one to one functions. An inverse function g^-1 exists for a function g if and only if g is one to one. The inverse function undoes the actions of the original function, and their graphs exhibit symmetry about the line y = x.

Steps to Find the Inverse of a One to One Function

Deriving the inverse function g^-1 for a one to one function g(x) involves the following steps:

1. Set g(x) equal to y.
2. Interchange x and y in the equation.
3. Solve for y to express it in terms of x.
4. Rename y as g^-1(x) to obtain the inverse function.

For example, if g(x) = 2x + 5, the inverse function g^-1(x) would be (x – 5)/2.

Conclusion

Understanding one to one functions is crucial in mathematics as they offer unique mappings between elements of sets. By grasping the properties and methods to identify one to one functions, individuals can delve deeper into the realm of functions and their inverses, paving the way for solving diverse mathematical equations.