Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Contents
Understanding the Radius of a Circle
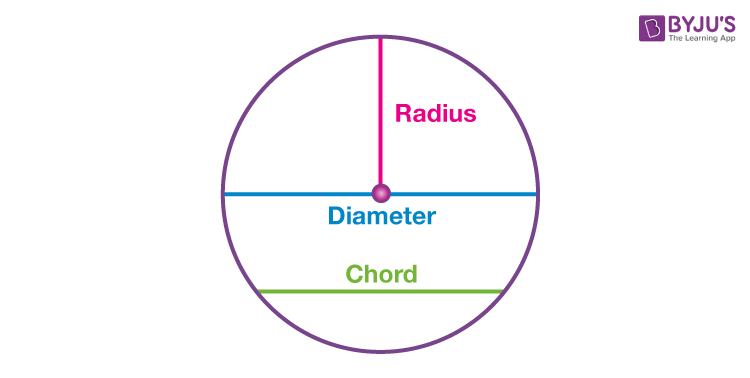
The radius of a circle is a fundamental concept in geometry, defining the distance from the center of the circle to any point on its circumference. It is denoted by ‘r’ and plays a crucial role in various circle-related calculations. The radius is half the length of the diameter and is essential in determining the area and circumference of a circle.
Radius, Diameter, and Chord
The diameter of a circle is the longest chord, passing through the center and connecting two points on the circumference. It is twice the length of the radius, denoted by ‘d’. The chord of a circle is any line segment with both endpoints on the circle. A chord passing through the center is the diameter, while a line perpendicular to a chord from the center bisects the chord.
Equation of a Circle
The equation of a circle with center (h, k) and radius ‘r’ is given by (x – h)² + (y – k)² = r². When the center is at the origin (0,0), the equation simplifies to x² + y² = r². This equation helps in plotting circles on the Cartesian plane.
Finding the Radius of a Circle
The radius of a circle can be determined using various formulas based on the information available. Whether you have the diameter, circumference, or area of a circle, there are specific formulas to calculate the radius accurately.
Radius from Diameter
When the diameter of a circle is known, the radius can be calculated using the formula: Radius = Diameter / 2. For instance, if the diameter is 16 cm, the radius would be 16 / 2 = 8 cm.
Radius from Circumference
If the circumference of a circle is given, the radius can be found using the formula: Radius = Circumference / (2 * π). For a circumference of 40 cm, the radius would be 40 / (2 * π) ≈ 6.37 cm.
Radius from Area
When the area of a circle is provided, the radius can be calculated as Radius = √(Area / π). For example, if the area is 78.54 sq cm, the radius would be √(78.54 / π) ≈ 5 cm.
Key Theorems Related to Circles
Theorem 1: Perpendicular Bisector
In a circle, the perpendicular line drawn from the center to a chord bisects the chord. This theorem is essential in understanding the properties of chords within a circle.
Theorem 2: Midpoint and Perpendicularity
If a line drawn through the center of a circle bisects a chord, it is perpendicular to the chord. This theorem highlights the relationship between the center, chord, and perpendicularity within a circle.
Conclusion
Understanding the radius of a circle is crucial in geometry and mathematics. It serves as a key parameter in various circle calculations, including area, circumference, and diameter. By applying the appropriate formulas and theorems related to circles, one can accurately determine the radius of a circle based on the available information.
